树 – Bryce's Blog

概念：

·根：没有父亲的节点
·树叶：没有儿子的节点
·兄弟节点：具有相同的父亲节点
·深度：从根到节点之间的唯一路径长度
·高度：从节点到所有树叶中最长的长度

基本分类：

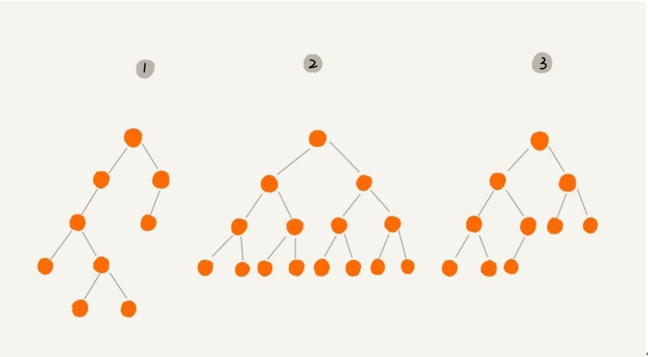
·二叉树(Binary Tree)：对于树中的每一个节点，最多有两个子节点。
·满二叉树(Perfect Binary Tree)：所有的叶子节点的深度相同，并且除了叶子节点每个节点都有左右两个子节点。
·完全二叉树(Complete Binary Tree)：从根节点到倒数第二层是满二叉树，最底层可以不填满，但是所有的叶子节点必须从左向右紧密排列。

图片源自https://time.geekbang.org/column/article/67856

除了用链表来实现，完全二叉树也可用数组来存储，把树从根节点开始依次从左到右放入数组。如果从索引为1的地方开始存，对于每个节点n来说，那么左节点就是2n，右节点就是2n+1（关于这个性质我只想到了用等比数列求和去推每个节点的编号，没想到其他直观的解释）（如果从索引为0的地方开始存也一样，只不过推导时多减个常数1而已，左边是2n+1，右边是2n+2）。

遍历：

二叉树的遍历本质上就是按一定逻辑把一个二维结构变成一个一维结构。
·前序遍历：对于树中任意节点，先访问该节点再访问左子树，最后访问右子树
·中序遍历：对于树中任意节点，先访问左子树再访问该节点，最后访问右子树
·后序遍历：对于树中任意节点，先访问左子树再访问右子树，最后访问该节点
·层序遍历：一层层从左至右遍历
二叉树非递归遍历的难点主要在于怎么保存暂时不访问的节点，以便让自己能回得去。

递归的比较简单，此处建议自己写一下每种遍历的非递归实现方式，再对比看看别人怎么写的。网上的前序和中序大部分思路都是这样： https://blog.csdn.net/coder__666/article/details/80349039（前序和中序只是print的位置变一下）。以下是在网上看的一段实现后序遍历的思路，在前两个的基础上改的，感觉写的很精妙，我加了点注释方便理解。

public void PostorderTraversal(TreeNode root) {
    Deque stack = new ArrayDeque();
    TreeNode last = null;  //指向上个节点
    while((root!=null)||(!stack.isEmpty())) {
        while(root!=null) {
	    stack.push(root);
	    root = root.left;
	}
	if(!stack.isEmpty()) {
	    root = stack.pop();
	    if((root.right==last)||(root.right==null)) {
	    //右子节点刚走完或右子节点为空都意味着目前所在的节点其左右子树都已经访问完了，可以访问现在所处的节点了
	        System.out.println(root.value); //访问节点
		last = root;
		root = null;  //该节点及其子树已全部访问完，指向空，然后再在上面切换到其父节点
	    }else {
	    //右子节点不为空则还不能访问现在所处的节点，所以又放回去
	        stack.push(root);
		root = root.right;
	    }
	}
    }
}

前面的思路大致都是用堆栈来把自己保存起来，然后去访问左儿子，访问完了再回来访问右儿子。除此以外也可以用队列来遍历，队列比较适合实现层序遍历。
思路：先把根节点放进队列，然后出队访问该节点，然后把左右儿子放进去，不断循环。

二叉搜索树 (BST,Binary Sort Tree)

概念：
二叉搜索树或者是一棵空树，或者是具有下列性质的二叉树：
　　1) 若左子树不空，则左子树上所有结点的值均小于它的根结点的值；
　　2) 若右子树不空，则右子树上所有结点的值均大于它的根结点的值；
　　3) 左、右子树也分别为二叉搜索树。

性质：
对二叉查找树进行中序遍历，即可得到有序的数列。

时间复杂度：
类似于二分查找，插入和查找的时间复杂度均为O(logn)，但是在最坏的情况下仍然会有O(n)的时间复杂度（在极端情况下，二叉搜索树退化为一条单链）。其搜索效率很容易受插入顺序的影响，而平衡二叉树在二叉搜索树的基础上解决了这个问题。

操作：
查找和插入都比较简单，删除要分情况讨论：
1）要删除的是叶结点：直接删除
2）要删除的只有一个孩子结点：将其父节点的指针指向要删除结点的孩子结点
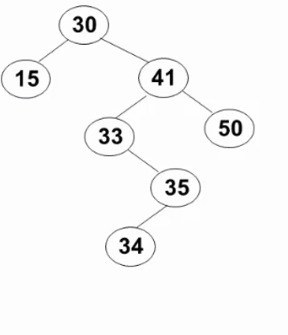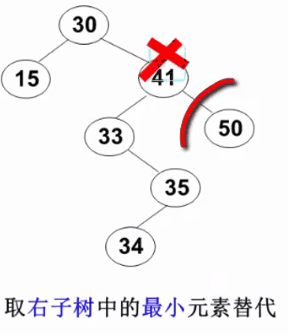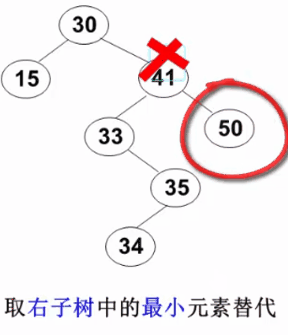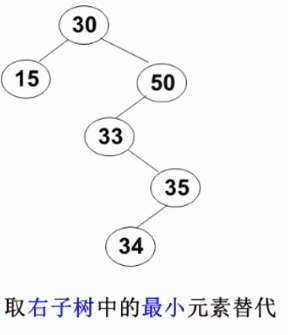
3）要删除的结点有左右两棵子树：用右子树的最小元素或左子树的最大元素替代被删除结点（以下示例图来自 https://www.icourse163.org/learn/ZJU-93001# ）

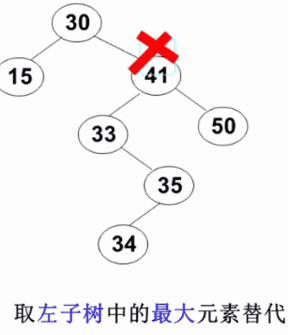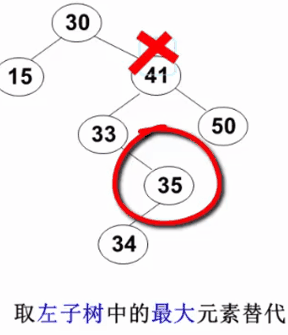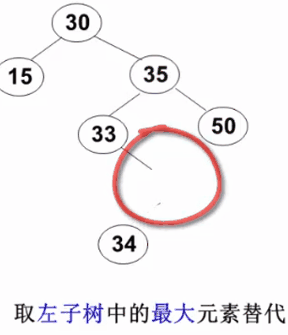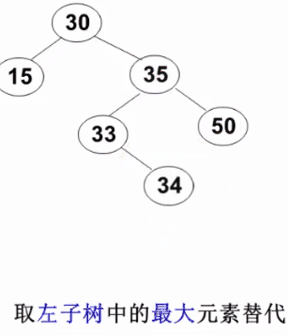
平衡二叉树 ( AVL树 )

概念：
· 平衡因子(Balance Factor)： BF(T) = hL – hR，其中 hL、hR 分别是左右子树的高度
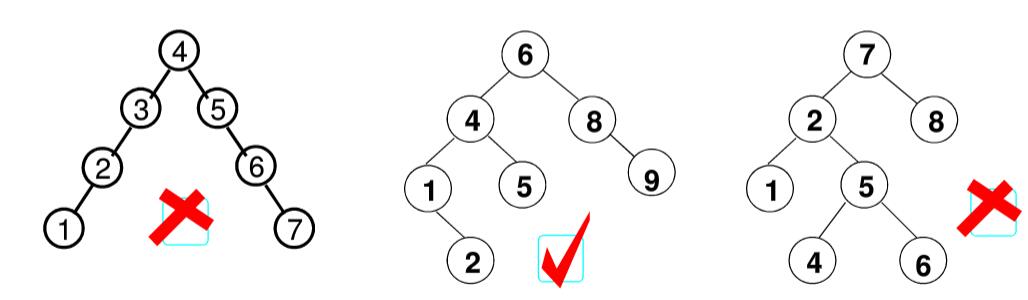
· 平衡二叉树(AVL 树) ：空树，或者任一结点左、右子树高度差的绝对值不超过 1，即 |BF(T)|≤1 的树

图片源自https://www.icourse163.org/learn/ZJU-93001#

调整

难点主要在于调整时要保持平衡以及保持二叉搜索树的性质。
调整时直接找最近的被破坏的平衡结点。

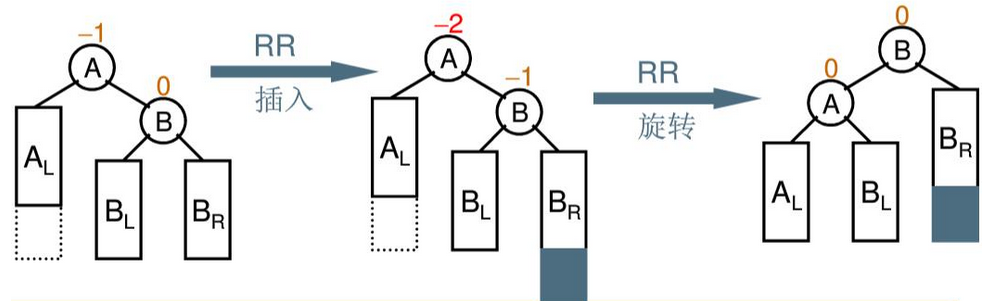
RR 单旋

当”插入结点”是”被破坏平衡结点”(A)右子树的右子树

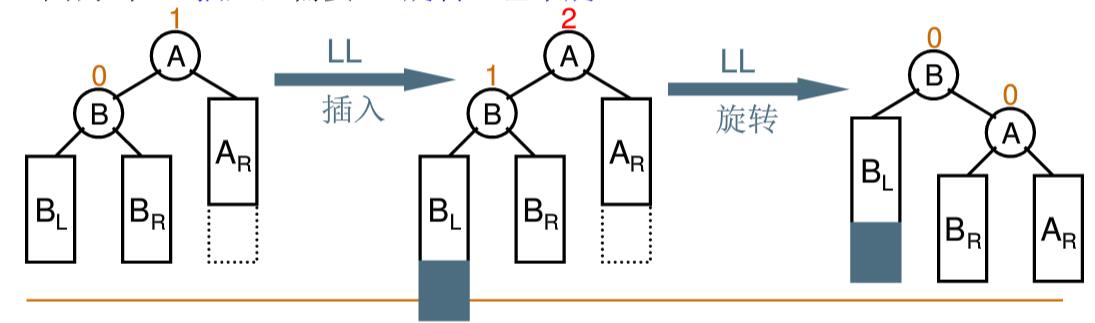
LL 单旋

当”插入结点”(BL)是”被破坏平衡结点”(A)左子树的左子树

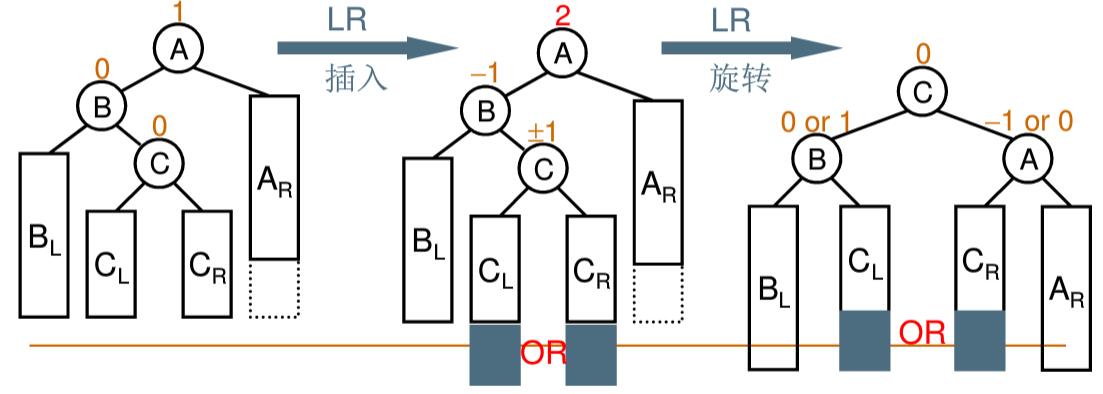
LR 双旋

当”插入结点”是”被破坏平衡结点”(A)左子树的右子树

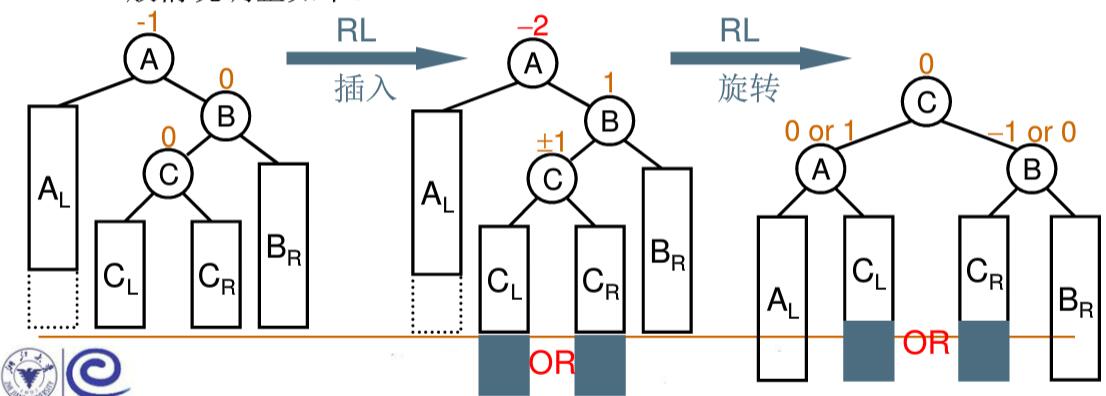
RL 双旋

当”插入结点”是”被破坏平衡结点”(A)右子树的左子树

堆

堆是一种特殊的树，只要满足下面两个条件，它就是一个堆：
（1）堆是一颗完全二叉树（所以用数组来存很合适）；
（2）堆中某个节点的值总是不大于（或不小于）其父结点的值。
其中，我们把根结点最大的堆叫做最大堆(MaxHeap)或大顶堆，根结点最小的堆叫做最小堆(MinHeap)或小顶堆。

从根结点到任意结点的路径都是有序的。

·插入：将插入元素与其父节点比较，若大于父节点则交换，不断重复直至不大于父节点或已成为根节点。
·取出最大/小：先把根结点取出来，然后把数组中最后一个元素从根结点开始从上往下比较，与左右儿子中的较大/小值比较，不断交换位置直至找到合适的位置。
·建堆：“取出最大/小”的思路就是把数组最后一个元素放到根结点，此时左右子树都是一个堆，然后通过调整把整个树其变成一个堆。“建堆”也可以参考这个思路，先从最后一个结点开始，把其和其兄弟节点（如果有的话）、父节点所在的树调成一个堆，这一层的其他节点也是，然后从底往上。这种方法的时间复杂度为O(n)。（具体实现可参考https://www.iteye.com/blog/shmilyaw-hotmail-com-1776612）

概念：